Triángulos

Triángulos

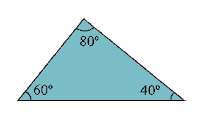
     Un triángulo es una poligonal cerrada con tres rectas que se cortan en tres puntos no alineados (vértices) y  posee tres ángulos interiores cuya suma siempre es de 180º.

                                     

Clasificación

Según sus ángulos 

Obtusángulo: triángulo que tiene un ángulo mayor de 90°.

Acutángulo:triángulo cuyos ángulos internos son menores a 90°.

Rectángulo: es un triangulo que posee un ángulo de 90º grados.

Según la longitud de sus lados

Equilátero: Todos sus lados miden lo mismo  y por lo tanto todos sus angulos son iguales.

Isósceles: Tiene dos lados iguales y uno desigual.

Escaleno: Los tres lados son desiguales.

Rectas y puntos notables de un triángulo


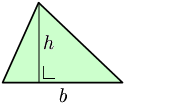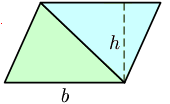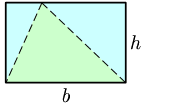
Altura: Es la recta que pasa por el vértice de un triángulo y es perpendicular al lado opuesto.

Mediana: son las tres rectas que unen cada vértice del triángulo con el centro del lado opuesto.

Mediatriz: Es la recta perpendicular que pasa por el punto medio de un lado del triángulo.

Bisectriz: son las rectas que dividen a cada ángulo, de los ángulos del triángulo, en dos ángulos iguales.

Ortocentro: punto donde se cortan las tres alturas de un triangulo.

Baricentro: punto de intersección de las medianas de cada uno de los lados.

Circuncentro: es el punto donde se cortan las mediatrices de los lados.

Incentro: punto de intersección de las bisectrices de cada uno de los ángulos.

  Fuentes: 1 2 3 4 5 6 7 8 

Nature by Numbers

     En el comienzo del video, durante la creación del caracol de mar, aparece la Sucesión de Fibonacci, la cual es utilizada para calcular el espiral del caracol. Ésta sucesión es una sucesión infinita de números naturales que tiene numerosas aplicaciones, desde las ciencias de la computación hasta en configuraciones biológicas.

     El video es bastante interesante, sobretodo la parte de la libélula, ya que demuestra que todo lo que existe puede ser explicado mediante modelos matemáticos.

    El Cálculo y sus aplicaciones 

     El cálculo es la matemática del cambio y el movimiento. Provee un marco para el modelo de sistemas en los que ocurre un cambio y una manera de deducir predicciones de estos mismos.

     El cálculo provee métodos para resolver dos grandes clases de problemas. El primero de estos involucra saber la frecuencia a la cual una cantidad variable cambia, por ejemplo, cuando un cuerpo viaja en línea recta, la distancia desde el punto de partida cambia a medida que pasa el tiempo y podríamos preguntarnos cuán rápido se está moviendo en algún instante específico. Llamamos a la rama del cálculo que trata con este tipo de problemas Cálculo Diferencial.

     Por otro lado, si nos dan la velocidad de un cuerpo en movimiento en cualquier momento, podríamos buscar la distancia que ha recorrido como una función del tiempo. Este otro tipo de problema, el de encontrar una función en la que su frecuencia de  cambio es conocida pertenece al dominio del Cálculo Integral.

     La ciencia moderna y la ingeniería usan ambas ramas del cálculo para expresar leyes físicas en términos matemáticos precisos  y estudiar sus consecuencias.

Fuente: Calculus and Analytic Geometry, Thomas/Finney, Fifth Edition.

El cálculo en la vida diaria

     Como experiencia personal con el cálculo, voy a tomar como ejemplo los auriculares.  Éste es un dispositivo de tipo transductor, es decir,  que puede transformar un tipo de energía de entrada, en otro de diferente a  la salida. Específicamente transforma impulsos  eléctricos  en una señal de ondas sonoras audible mediante una serie de mecanismos.

     El cálculo está presente en este dispositivo debido a que “la frecuencia de una onda sonora depende de con que periodicidad vibren las partículas del medio, en el momento en que este es atravesado por una onda. Dicha frecuencia es medida según el número de vibraciones completas de una partícula del medio por unidad de tiempo. Si una partícula de aire experimenta 1000 vibraciones longitudinales durante 2 segundos, entonces, la frecuencia de la onda es de 500 vibraciones por segundo”.  Elementos como las ondas sonoras, el tiempo y las partículas del medio representan las variables y la frecuencia de una onda sonora representa una función.

Fuente 1/Fuente 2

En la ingeniería civil

     En la construcción de una estructura como un edificio alto o un rascacielos la aplicación del cálculo se siente en numerosos aspectos, por ejemplo, el viento que circula por la zona en la que es construida la estructura es un factor que actúa como variable, ya que  características como la velocidad, el ángulo de incidencia, la densidad, entre otros, tienen la capacidad de influir en gran parte de las características de la obra como los materiales, las medidas, la forma de la estructura, el ángulo de construcción, etc .

Fuente